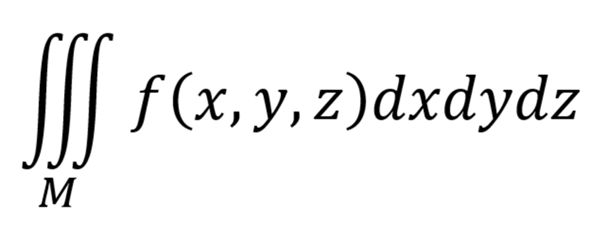Integral de volumen

En matemáticas (particularmente en el Cálculo en Varias Variables), una integral de volumen se refiere a una integral sobre un dominio tridimensional; esto es, es un caso especial de las integrales múltiples. Las integrales de volumen son especialmente importantes en la física pues se tienen muchas aplicaciones, un ejemplo de ello es que son utilizadas para calcular la densidad de flujo.

En coordenadas

También puede hacer referencia a una integral triple sobre de una región ${\displaystyle D\subset \mathbb {R} ^{3}}$ de una función ${\displaystyle f(x,y,z),}$ y es normalmente escrita como

${\displaystyle \iiint _{D}f(x,y,z)\,dx\,dy\,dz.}$

Una integral de volumen en coordenadas cilíndricas es

${\displaystyle \iiint _{D}f(\rho ,\varphi ,z)\rho \,d\rho \,d\varphi \,dz,}$

Y en coordenadas esféricas es de la forma

${\displaystyle \iiint _{D}f(r,\theta ,\varphi )r^{2}\operatorname {sen} \theta \,dr\,d\theta \,d\varphi .}$

Véase también

• Teorema de divergencia
• Integral de superficie

Enlaces externos

• Hazewinkel, Michiel, ed. (2001), «Integral de volumen», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Weisstein, Eric W. «Volume integral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.